CUET EXAM Maths Previous Year Questions Set 1
CUET Maths 2023 Set 1
(i) The angle between the line 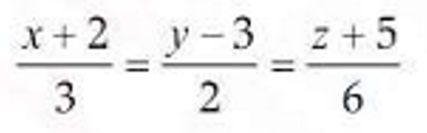 and the plane 2x + 10y — 11z = 5 is:
and the plane 2x + 10y — 11z = 5 is:

Solution
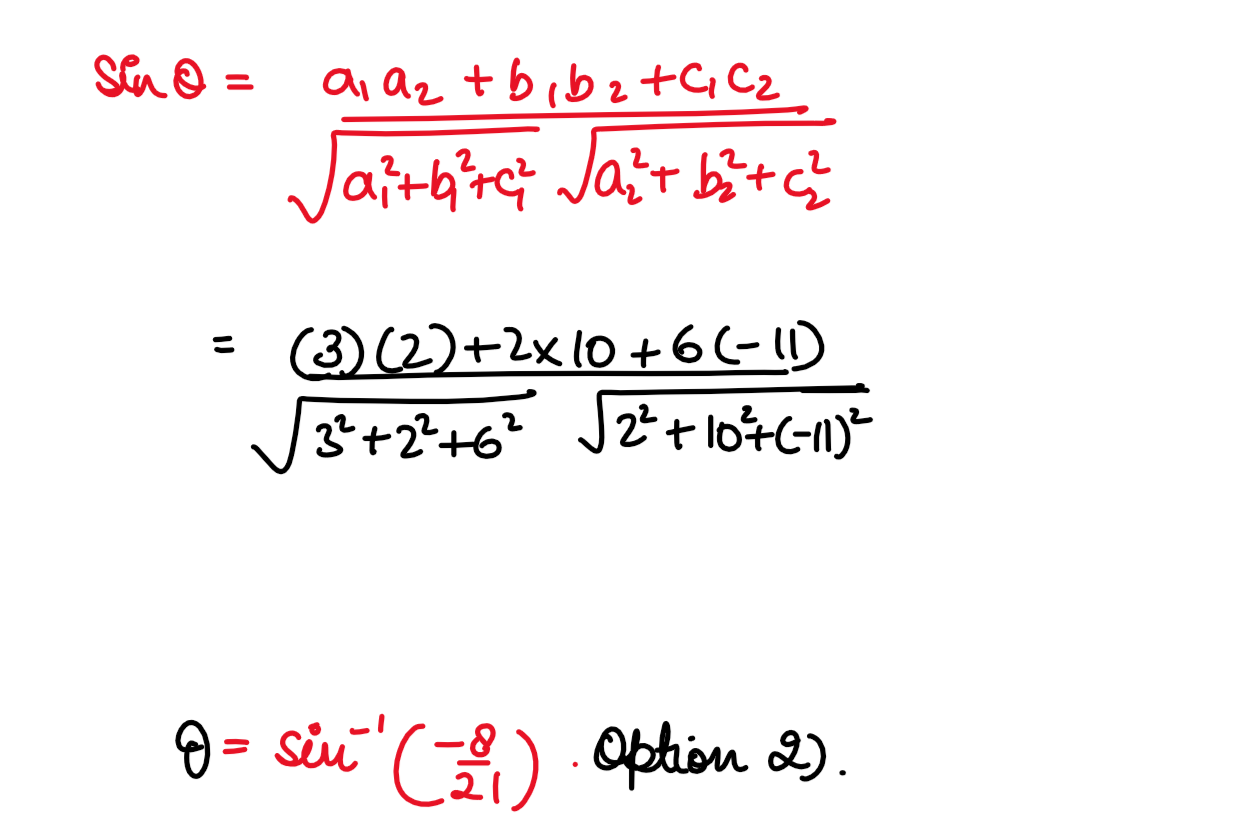
(ii) If matrix A is of order 2 x 3 and B of order 3 x 2, then
(1) AB, BA both defined and are equal
(2) AB is defined but BA is not defined
(3) AB is not defined but BA is defined
(4) AB, BA are defined but are not equal
Solution
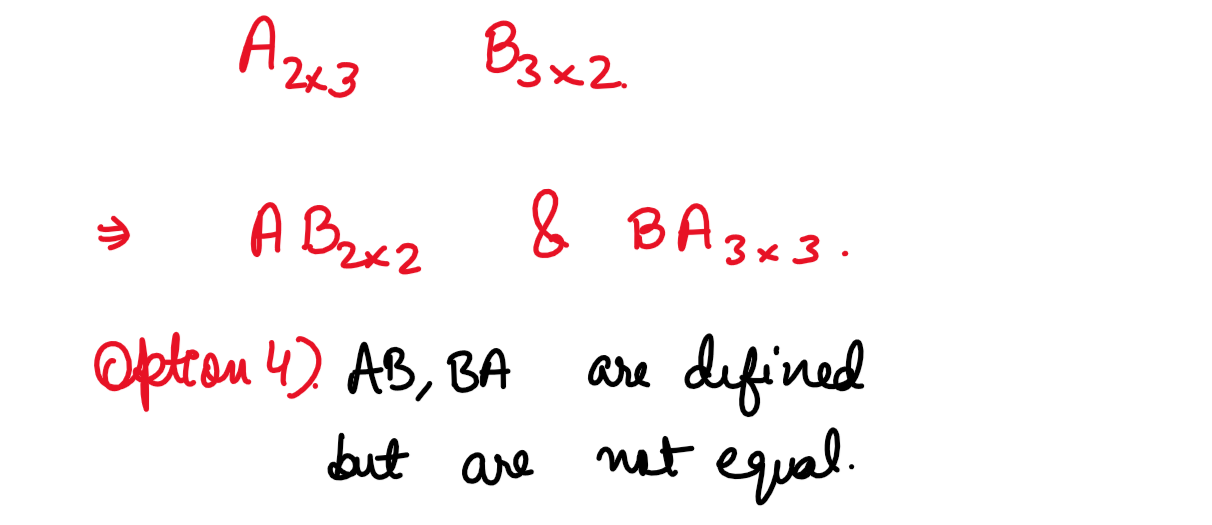
(iii) If A is a square matrix of order 3, B=kA and |B| =kA then,
(1) x=2k
(2) x=k2
(3) x=k3
(4) x=3k
Solution
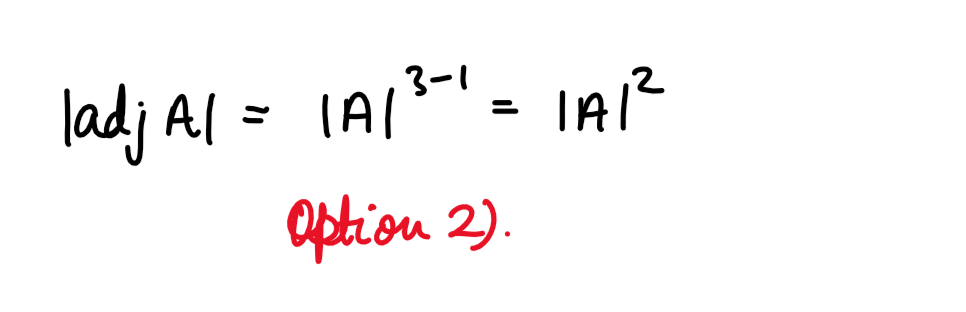
(iv) The degree Of the differential equation
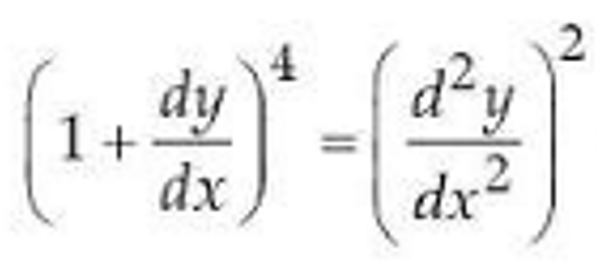
(1) 1
(2) 3
(3) 2
(4) 4
Solution

(v) The differential equation 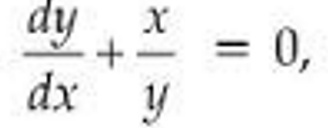 represents the family Of curves:
represents the family Of curves:
(1) x2-y2=c
(2) x/y=C
(3) xy=c
(4) x2>+y2>=C
Solution

(vi) If 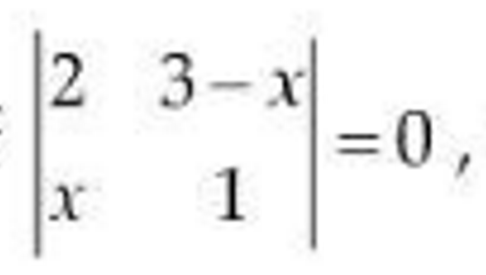 then the values of x are:
then the values of x are:
(1) 1 and 3
(2) 1 and 2
(3) 2 and 3
(4) 3 and 0
Solution
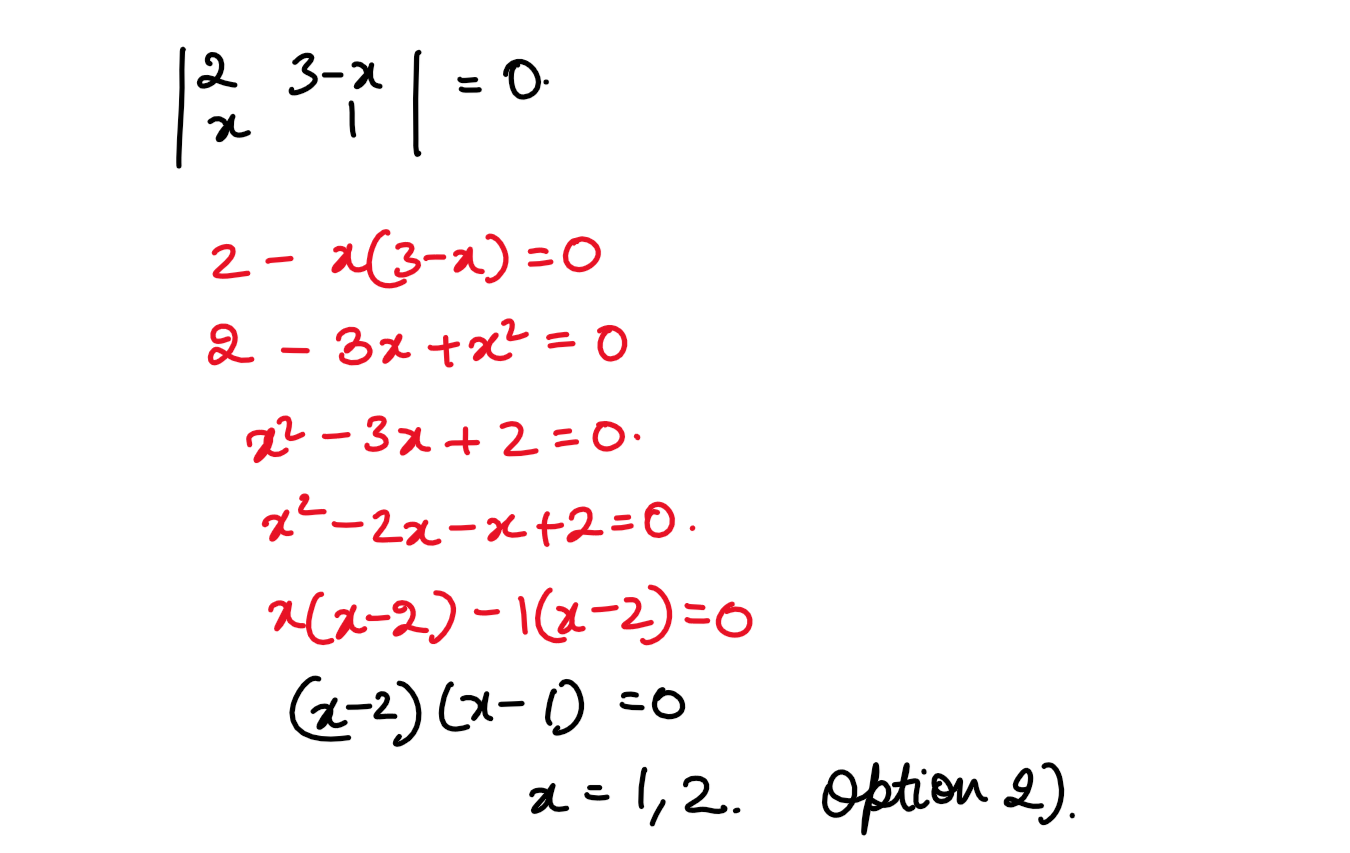
(vii) 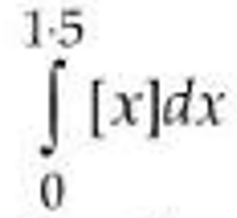 where [x] denotes the greatest integer
function ≤ x is equal to:
where [x] denotes the greatest integer
function ≤ x is equal to:
(1) 1/4
(2) 1/2
(3) 1
(4) 0
Solution
(viii) In a box containing 100 bulbs. 10 are defective.
Then the probability, that out of a sample of 5 bulbs
none is defective, is:
(1) 10-1
(2) (1/2)5
(3) (9/10)5
(4) (9/10)
Solution
(ix) If y=1/x+1, then d2y/dx2 at x=2 is:
(1) 2/9
(2) 3/2
(3) 2/27
(4) 3/8
Solution

(x) The matrix A= 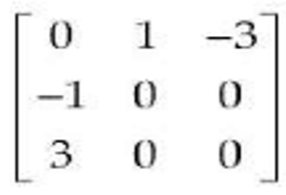 is a
is a
(1) Diagonal matrix
(2) Symmetric matrix
(3) Skew-symmetric matrix
(4) Scalar matrix
Solution

(xi) 
Choose the correct answer trom the options given
below:
(1) A-IV,B-II,C-I,D-III
(2) A-III,BIV,C-I,D-II
(3) A-I,B-II,C-III,D-IV
(4) A-II,b-III,C-IV,D-I
Solution

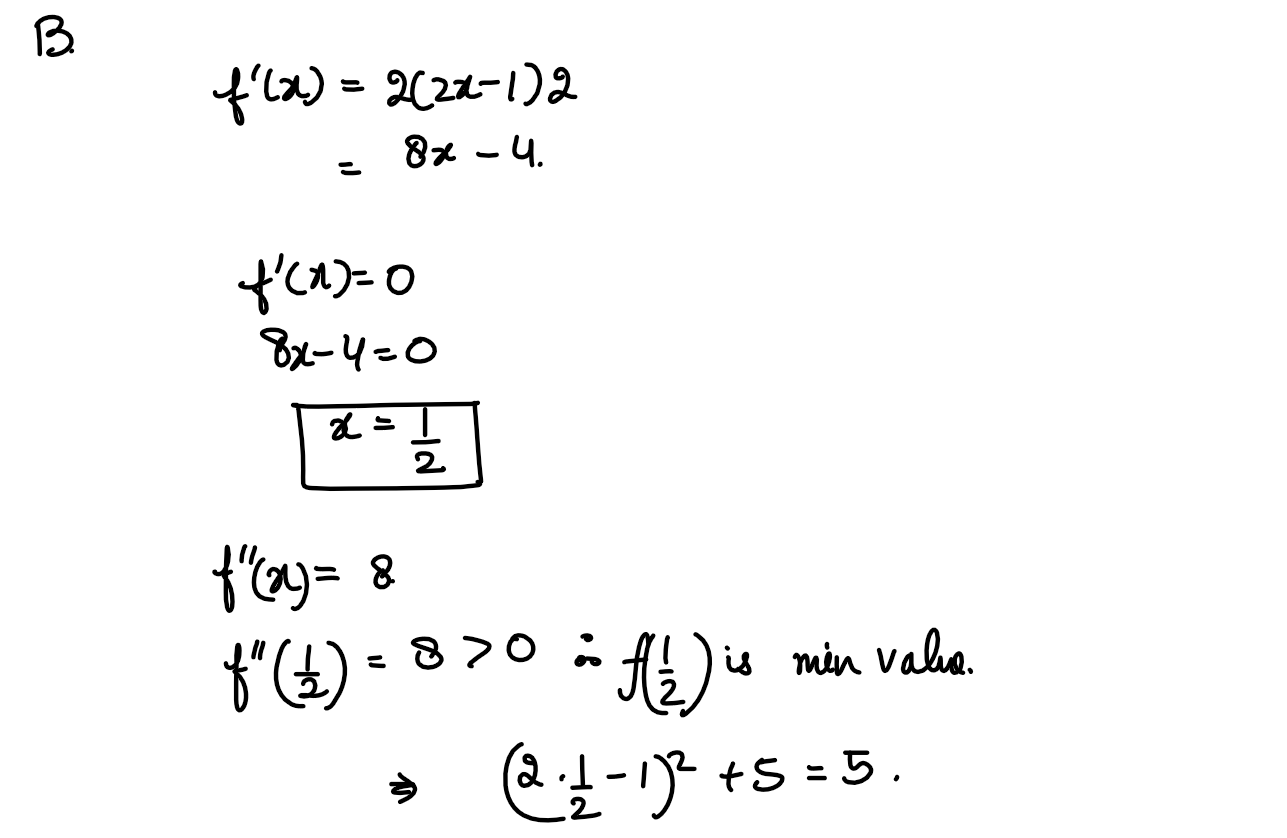
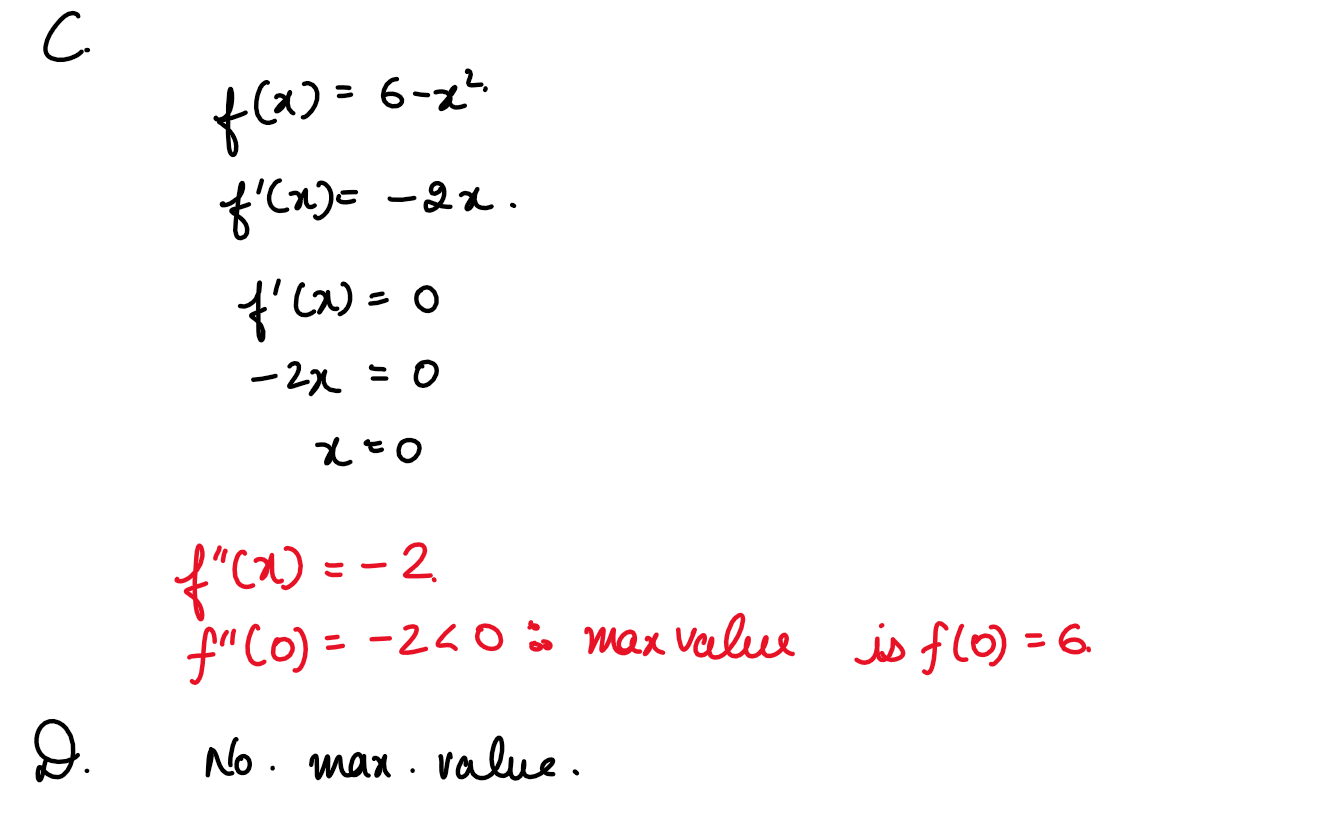
(xii) The mean number of heads in two tosses of a coin
(1) 2
(2) 1/2
(3) 1
(4) 3/2
Solution
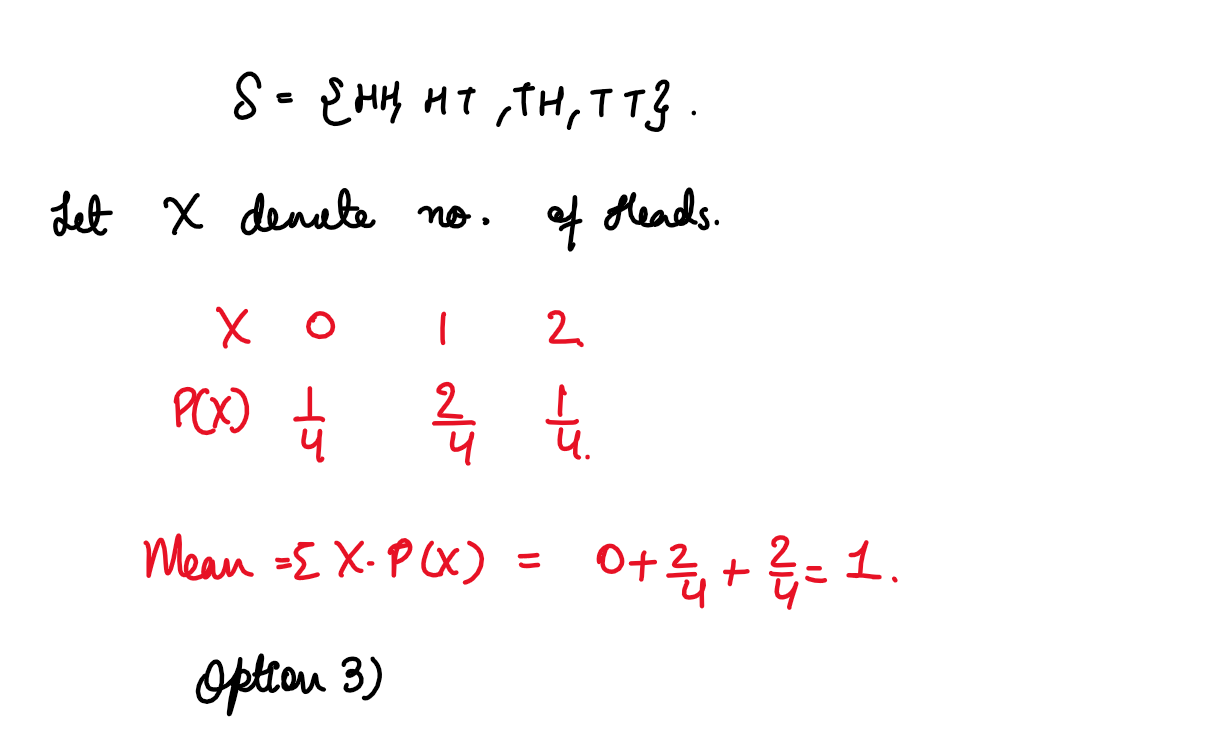
(xiii) If f(x)=1/1-x,then for x >1,f(x) is:
(1) decreasing
(2) constant
(3) increasing
(4) neither decreasing nor increasing
Solution

(xiv) The area enclosed by the ellipse 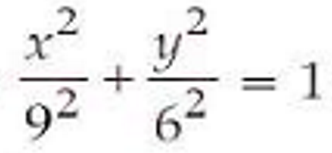 is:
is:
(1) 15π
(2) 54 π
(3) 18π
(4) 3/2 π
Solution

(xv) The solution of a LPP with basic feasible solutions
(0, 0), (10, 0), (0, 20). (10, 15) and objective function
Max Z=2x+3y is:
(1) x=0,y=20,Max Z=60
(2) x=10,y=15,Max Z=65
(3) x=10,y=20, Max Z=70
(4) x=15,y=10, Max Z=60
Solution
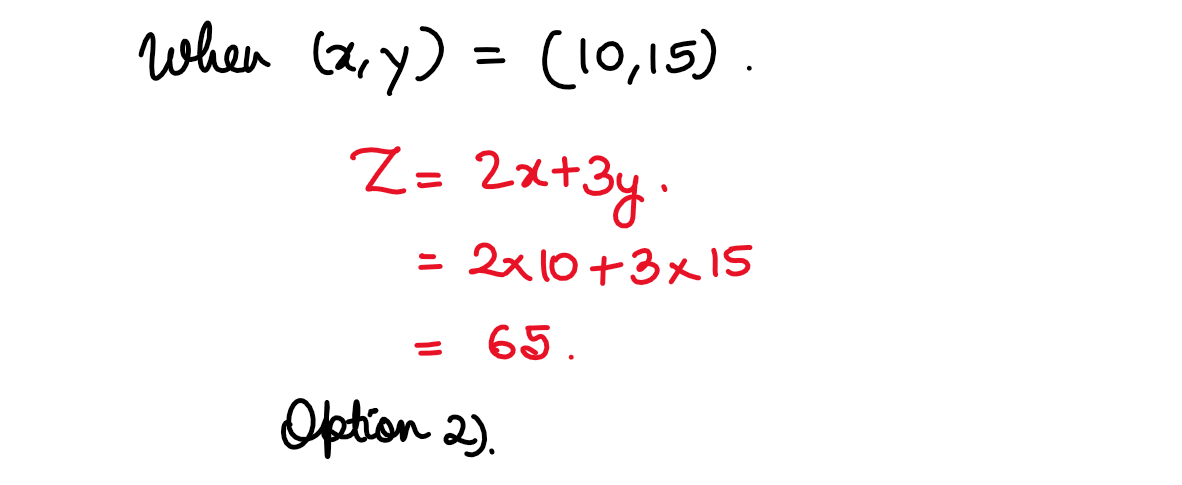
(xvi) In a meeting, 70% of the members favour and 30%
oppose a certain proposal. A member is selected
at random and we take X=O if he opposed. and
X= I if he is in favoul% Then. E (X) is:
(1) 7/10
(2) 1/2
(3) 1/3
(4) 7/11
Solution
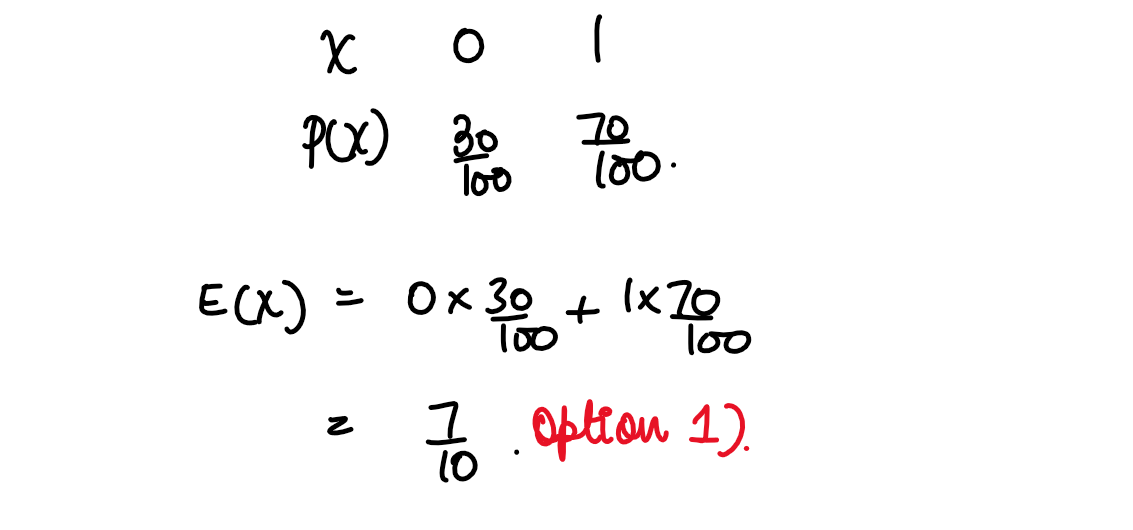
(xvii) The linear constraints, for which the shaded area
in the figure is the feasible region of an LPR are:
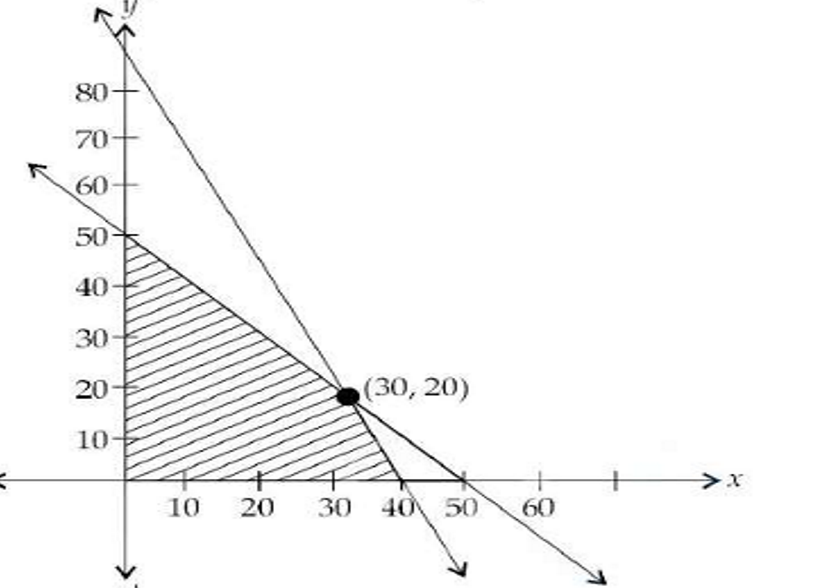
(1)
x +y≥50
2x + y≤80
x + y≥0
(2) x + y≤50
2x + y≥80
x + y≥0
(3) x + y≤50
2x + y≤80
x + y≥0
(4) x + y≥50
2x + y ≥80
x + y≥0
Solution
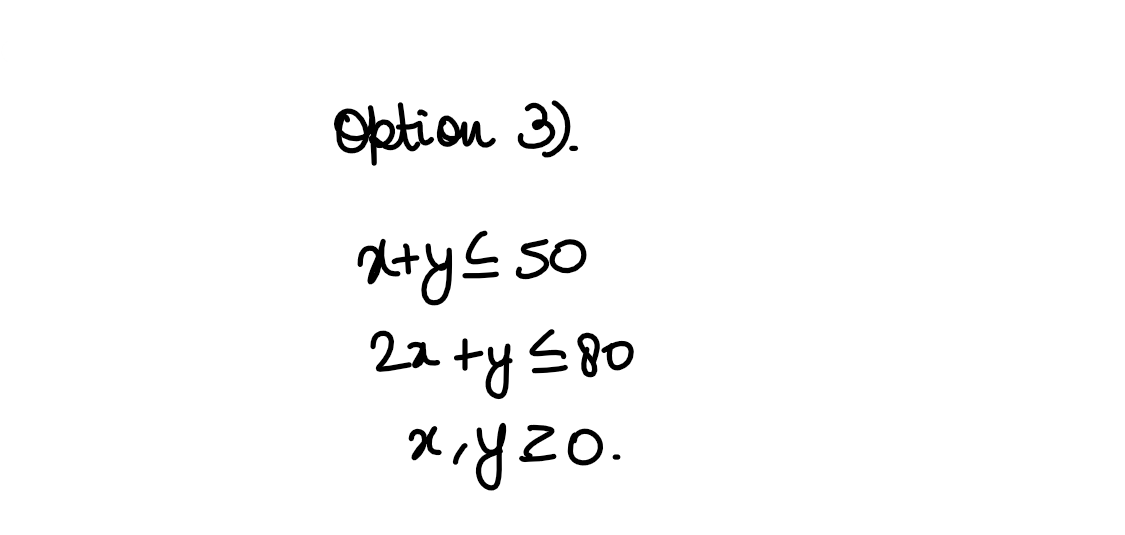
(xviii) Two dice are thrown simultaneously. If X denotes
the number of sixes, then the variance of X is:
(1) 5/18
(2) 7/18
(3) 1/3
(4) 2/3
Solution


(xix) If f:R->R is defined by f(x) = sin x + x. then f(f(x)) is:
(1) 2 sinx + 2x
(2) sin2x+x2
(3) sin (sinx+x) + sinx+x
(4) sin2x + 2sinx +x
Solution
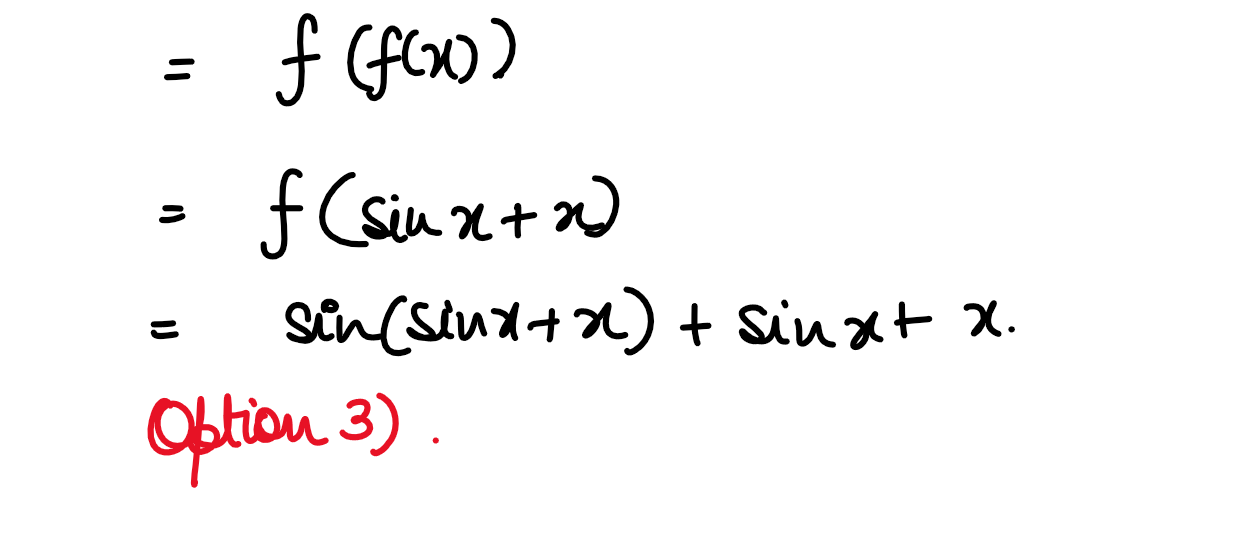
(xx) Which of the following statements is NOT
CORRECT.
(1) A row matrix has only one row.
(2) A diagonal matrix has all diagonal elements
equal to zero.
(3) A symmetric matrix is a square matrix satisfying
certain conditions.
(4) A skew-symmetric matrix has all diagonal
elements equal to zero.
Solution

(xxi) 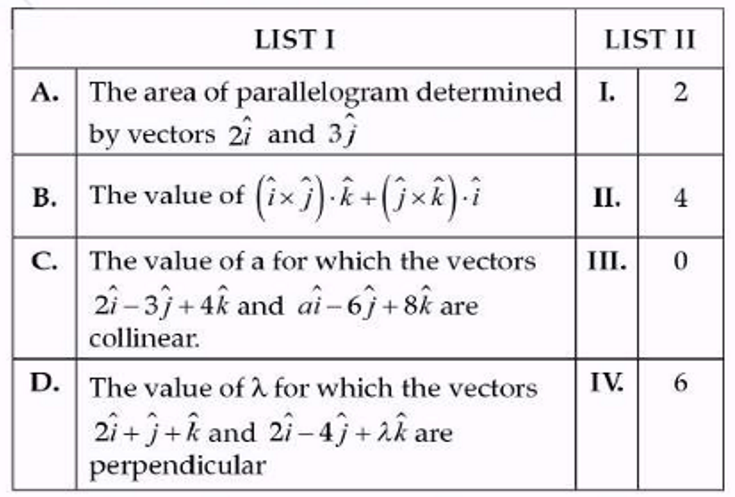
Choose the correct answer from the option given below:
(1) A-I,B-II,C-III,D-IV
(2) A-II,B-I,C-III,D-IV
(3) A-III,BIV,C-II,D-I
(4) A-IV,b-I,C-II,D-III
Solution


(xxii) 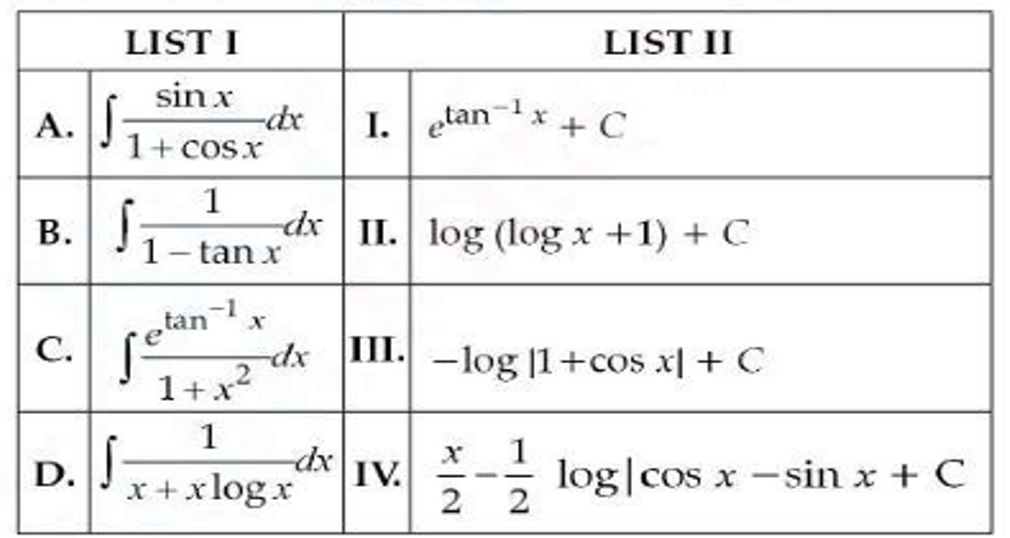
Choose the correct answer from the option given below:
(1) A-II,B-III,C-IV,D-I
(2) A-III,BIV,C-I,D-II
(3) A-I,B-II,C-III,D-IV
(4) A-IV,b-I,C-III,D-II
Solution
(xxiii) The function f(x)= x-1/x(x2-1),x≠1,f(1)=1, is
discontinuous at:
(1) Exactly one point
(2) Exactly two points
(3) Exactly three points
(4) No point
Solution
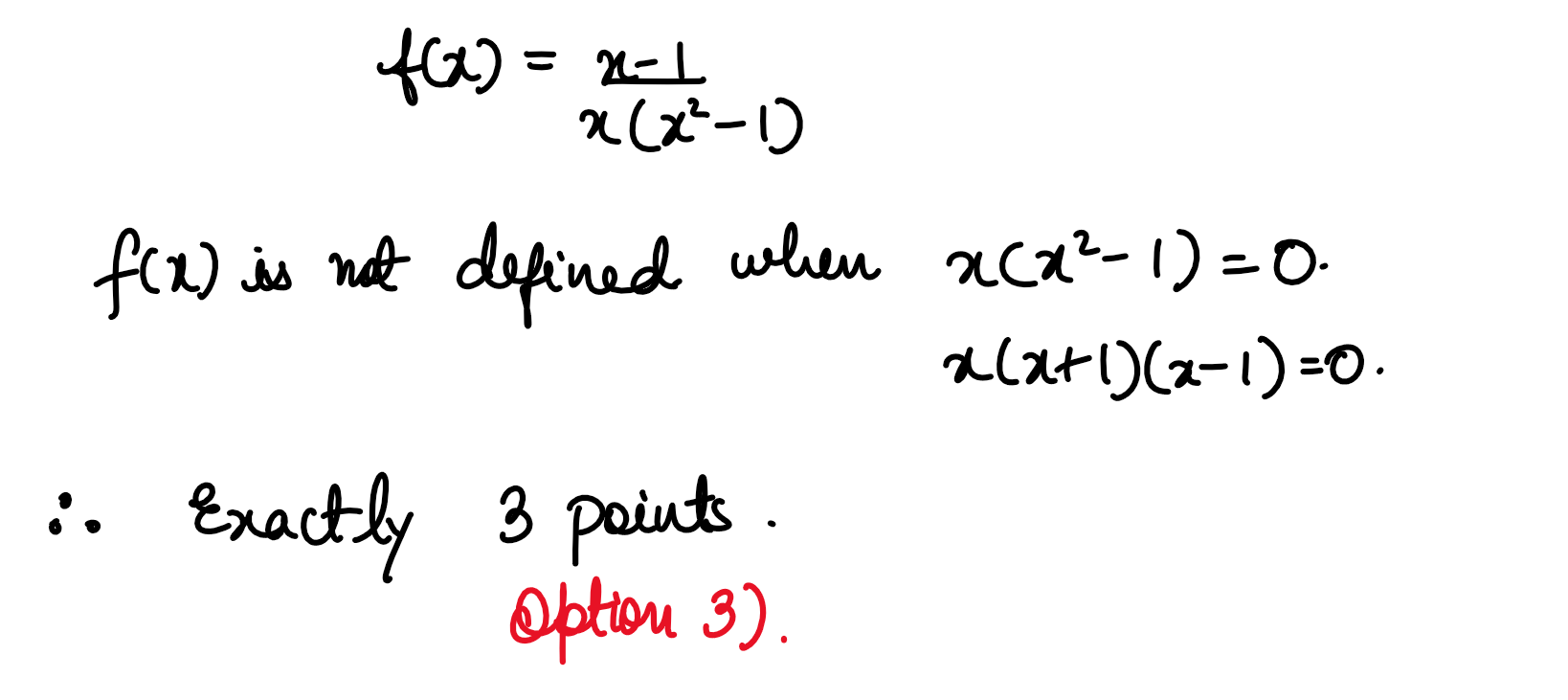
(xxiv) The area of the region bounded by the lines x=2y +3,x=0, and y=-1 is:
(1) 4 sq. units
(3) 8 sq. units
(2) 6 sq. units
(4) 3/2 sq. units
Solution
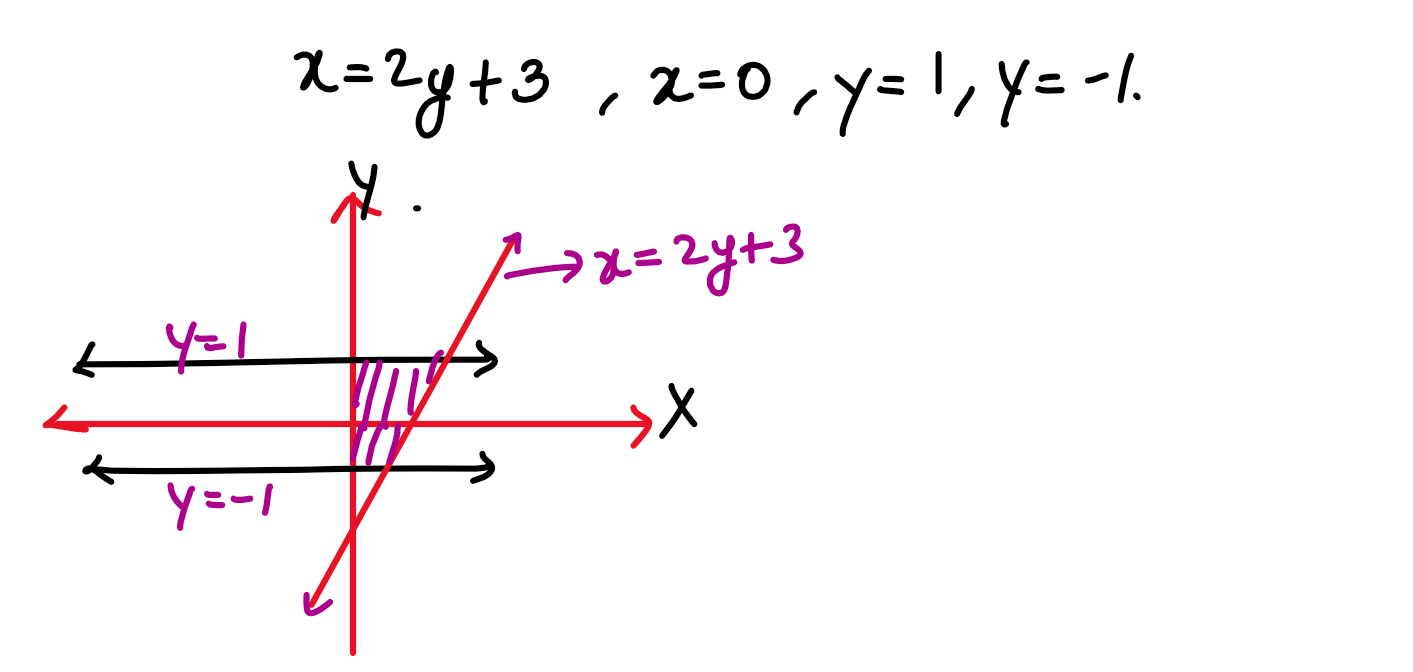
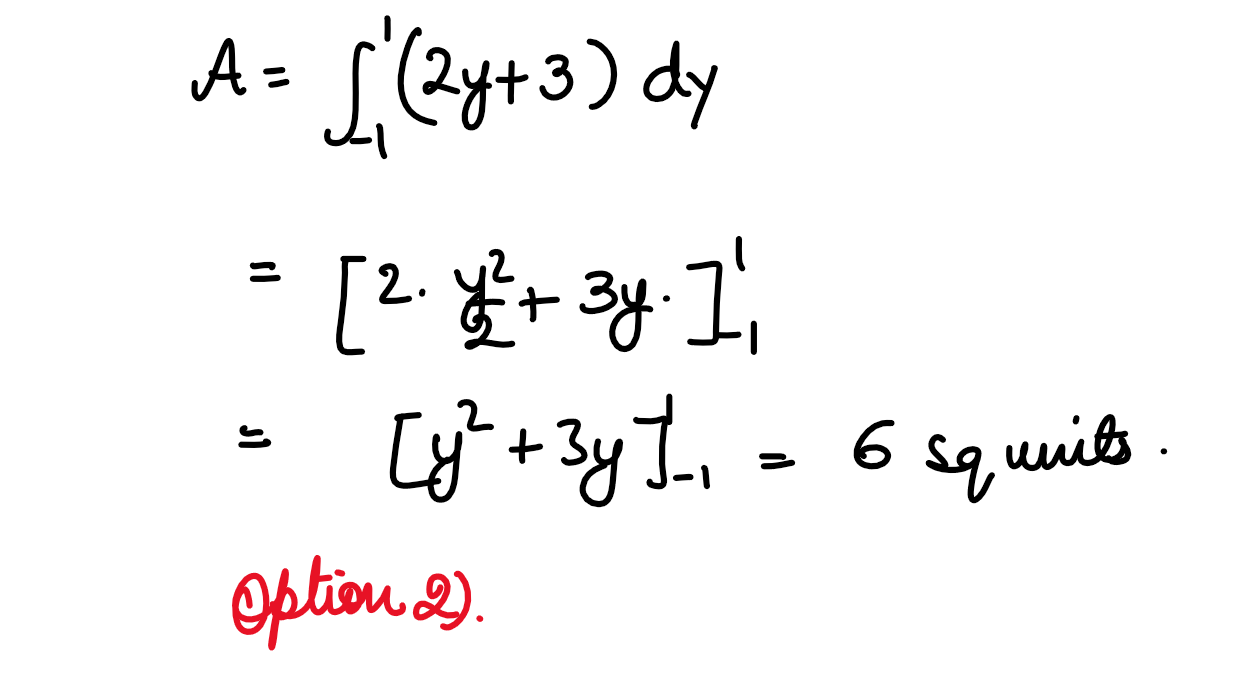
(xxv) The area of the region bounded by the parabola y2 = 4ax and its latus rectum is:

Solution

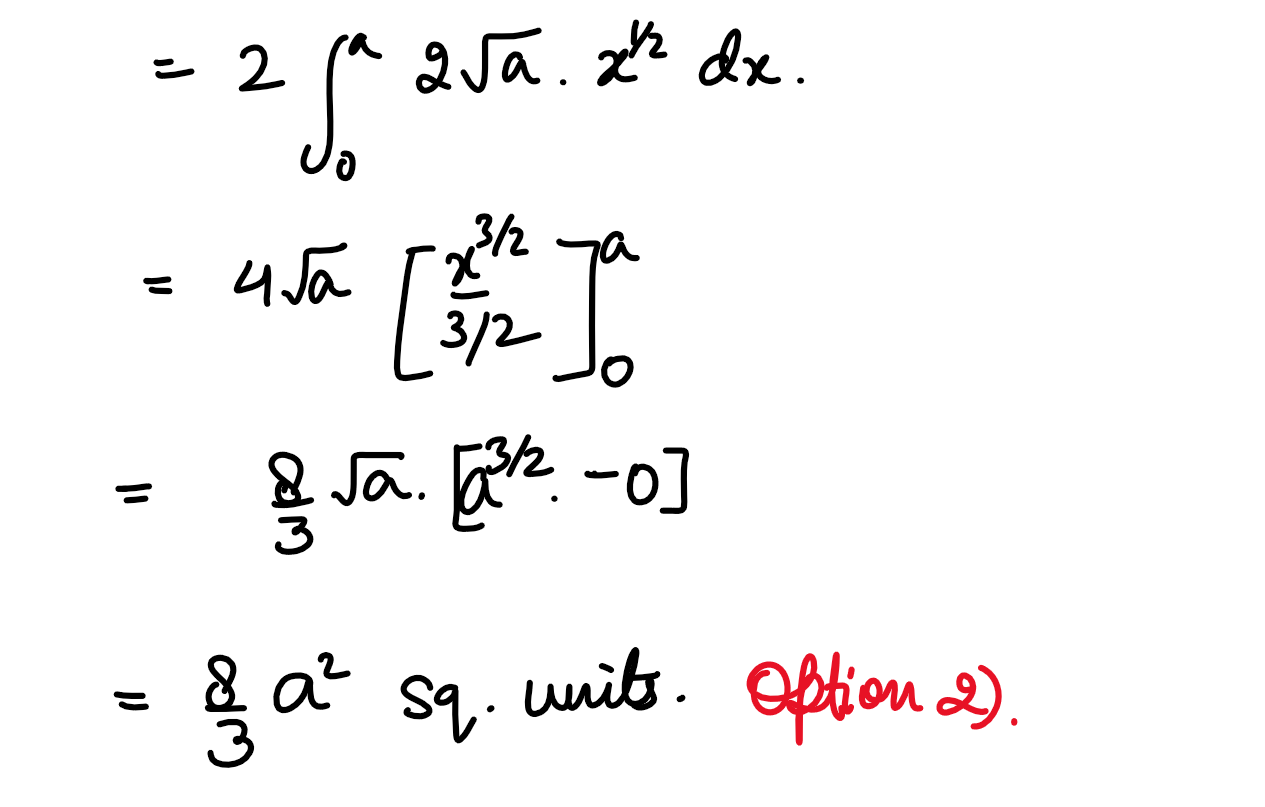
(xxvi) If the matrix  then A2 is equal
then A2 is equal
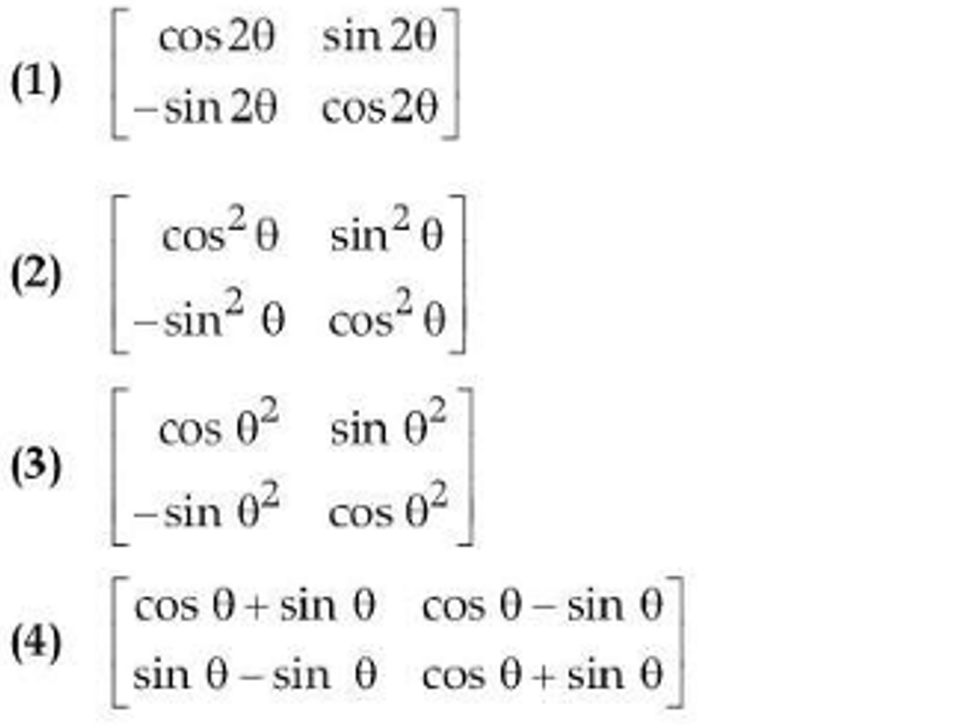
Solution

(xxvii) The maximum slope of the curve
y= -x3 + 3x2 - 27 is:
(1) 0
(2) 12
(3) 16
(4) 32
Solution
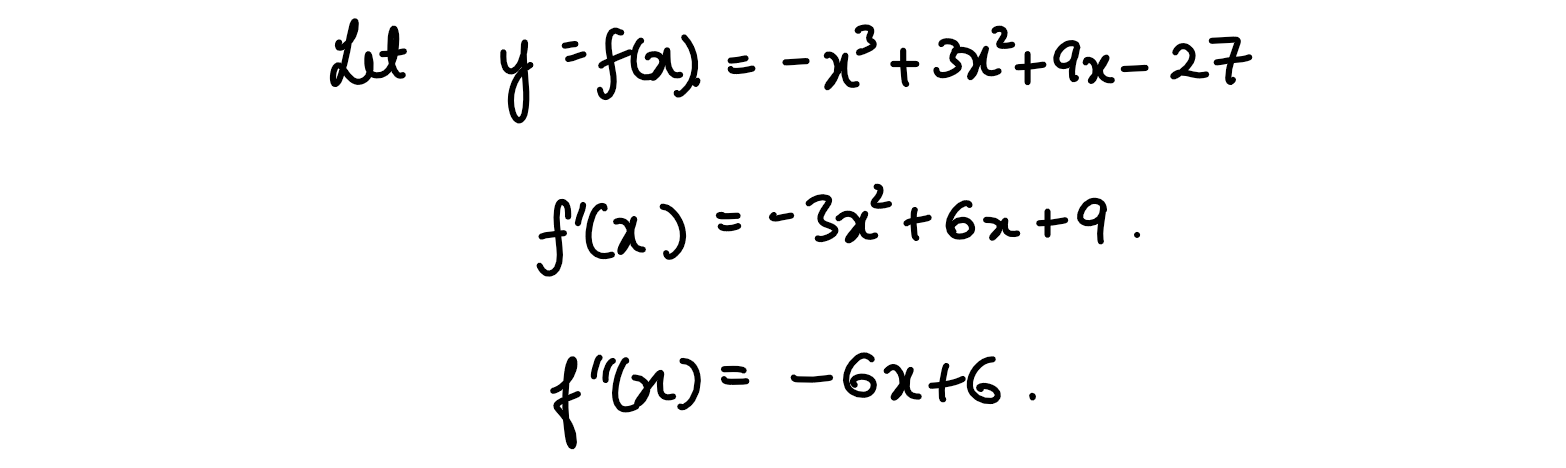

(xxviii) The approximate volume of a cube of a side a metres on increasing the side by 4% is:
(1) 1.04a3m3
(2) 1.004a3m3
(3) 1.12a3m3
(4) 1.12a2m3
Solution
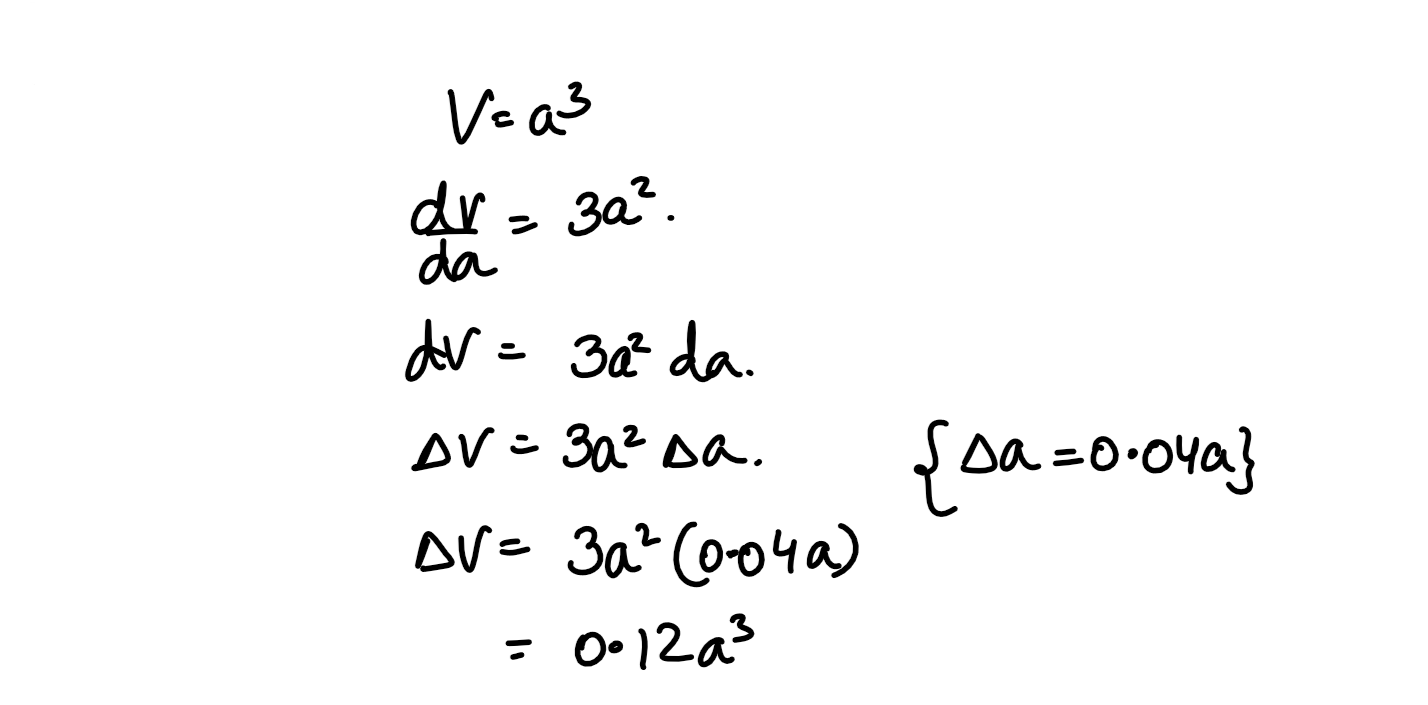
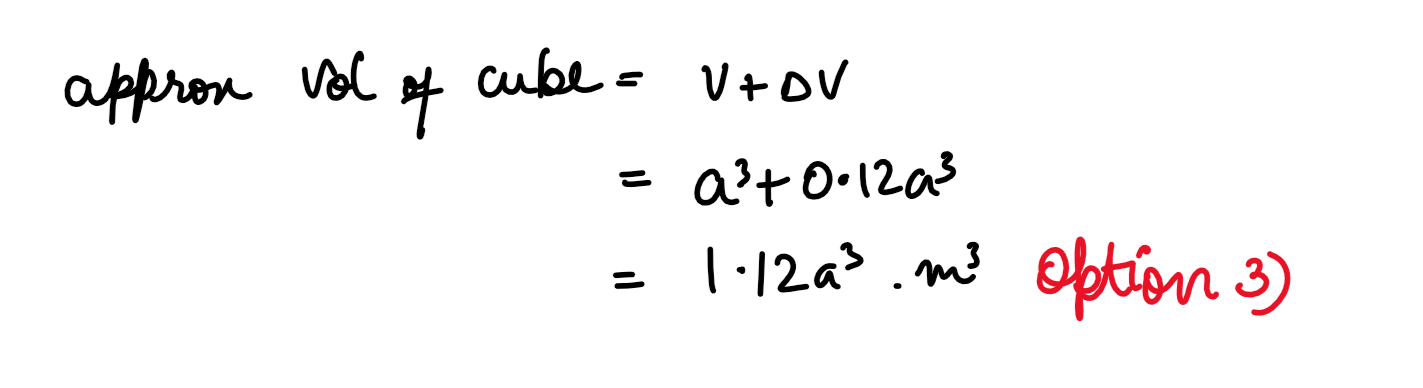
(xxix) 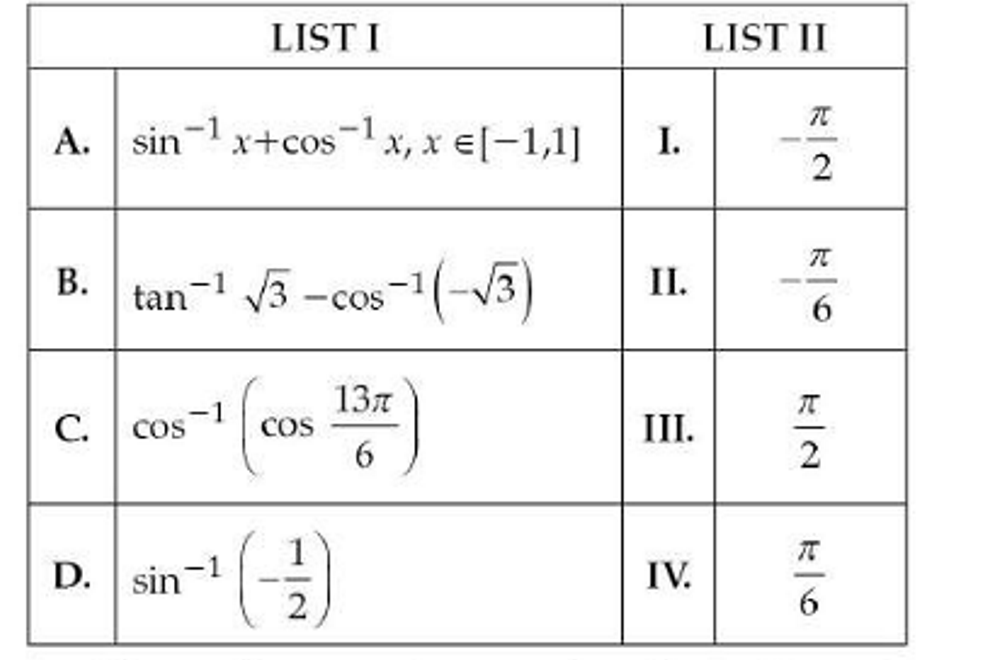
Choose the correct answer from the option given below:
(1) A-III,B-I,C-IV,D-II
(2) A-IV,b-I,C-II,D-III
(3) A-II,b-III,C-IV,D-I
(4) A-I,B-II,C-III,D-IV
Solution
(xxx) If the matrix A =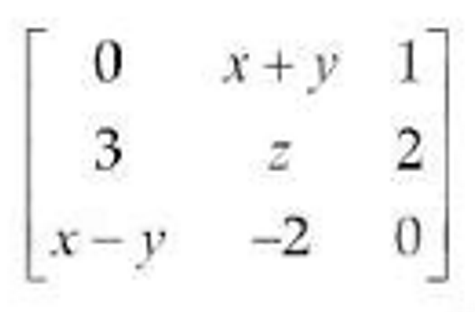 is skew-symmetric, then :
is skew-symmetric, then :
(1) x=2,y=1,z=0
(2) x=2,y=2,z=0
(3) x=-2,y=-1,z=0
(1) x=-2,y=-1,z=-1
Solution
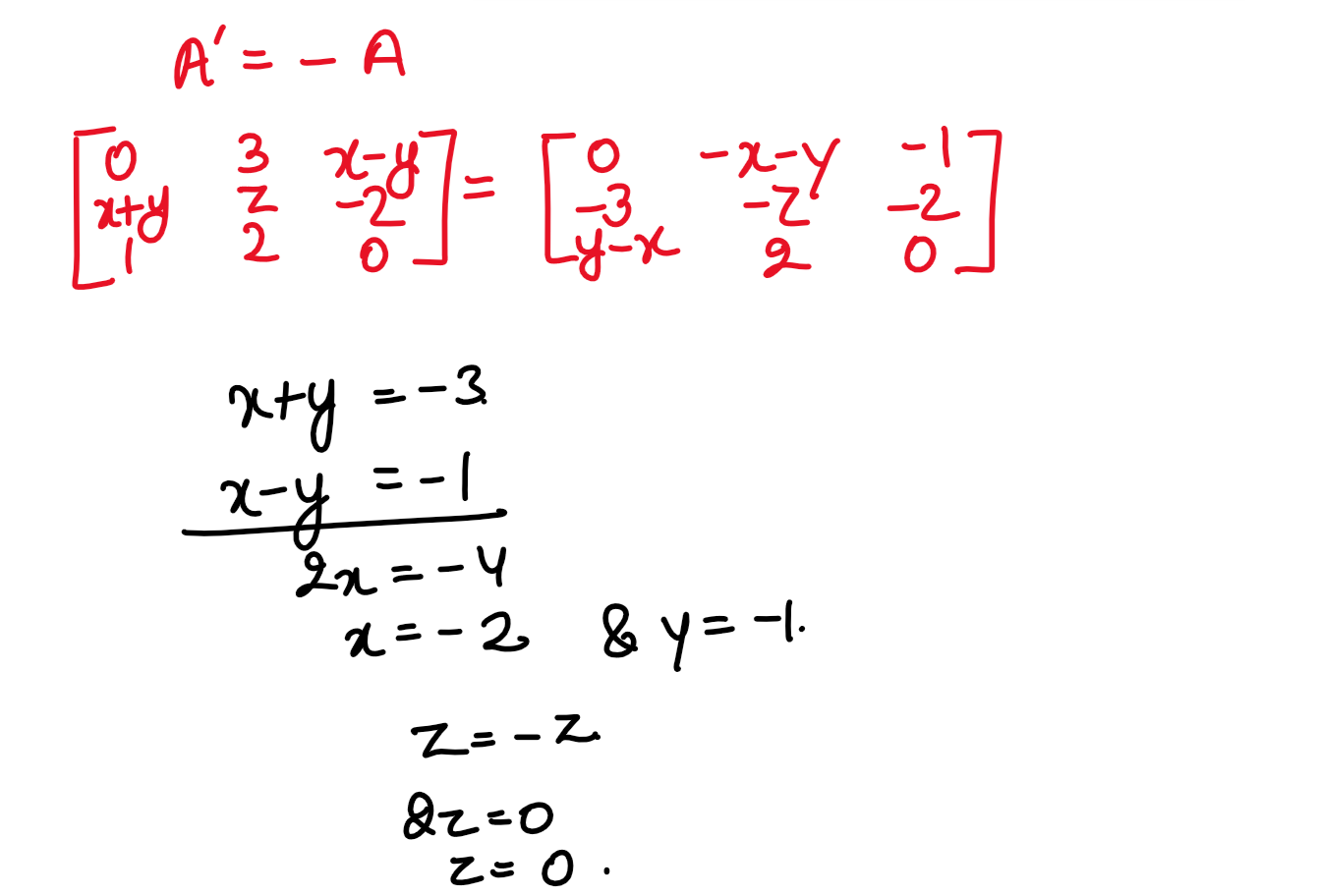
(xxxi) If three points A(a1, b1), B(a2, b2) and are
collinear and 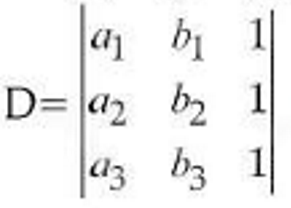 then:
then:
(1) D=0
(2) D=±1
(3) D2=0 or 1
(4) D=(a1+a2+a3)-(b1+b2+b3)
Solution
(xxxii) If a line makes angles 90°. 60° and θ with X and Y and
Z axis respectively, where 0 is acute, then value of
θ is:
(1) π/6
(2) π/4
(3) π/3
(4) π/2
Solution

(xxxiii) Particular solution of the differential equation
log(dy/dx)=x+y given that when x=0,y=0 is:
(1) ex + e-y=2
(2) e-x + ey=2
(3) ex + ey=2
(4) e-x + e-y=2
Solution
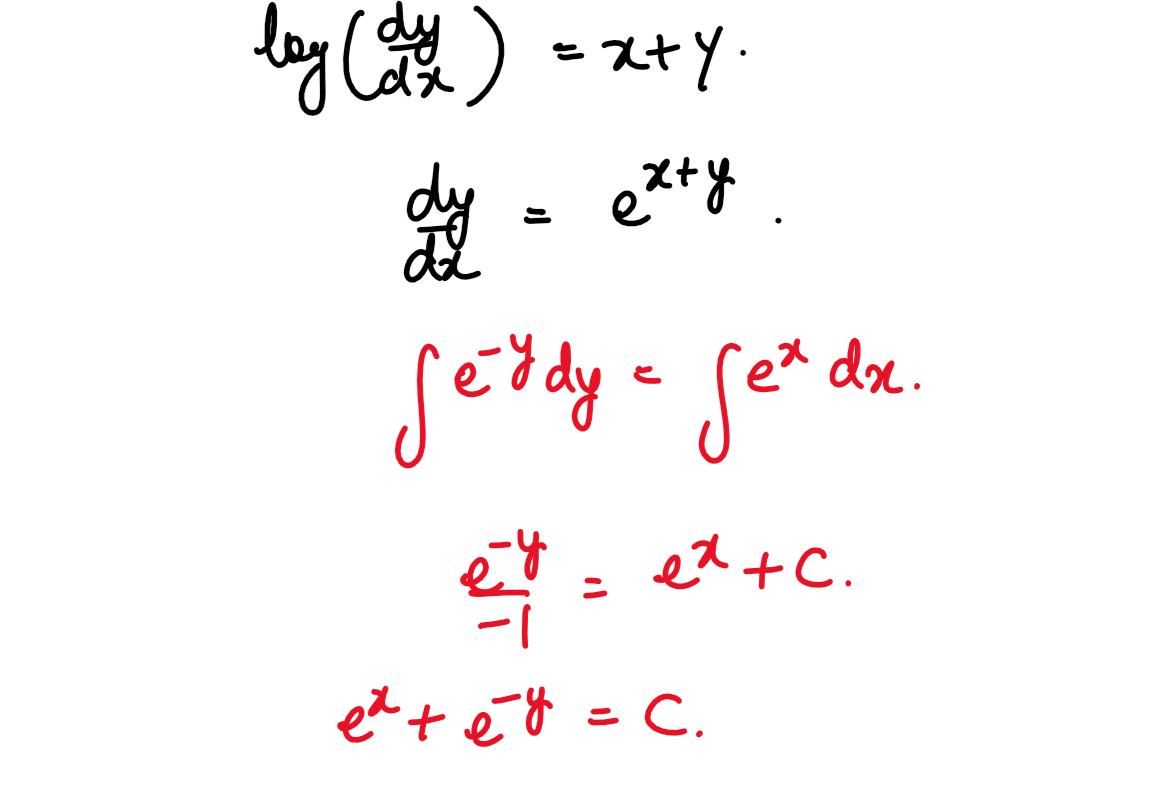

(xxxiv) Solution of dy/dx=(1+x2)(1+y2) is:
(1) tan-1y=x+x3/3 +c
(2) tan-1y=x5+x3/3 +c
(3) tan-1y=x2+x3/3 +c
(4) tan-1y=x4+x3/3 +c
Solution

(xxxv) A manufacturer can sell x items at a price of ₹3x+5
each. The cost price of x items is ₹x2 +5x. If x is the
number of items she should sell to get no profit
and no loss. then:
(1) x=10
(2) x=30
(3) x=0
(4) x=-10
Solution
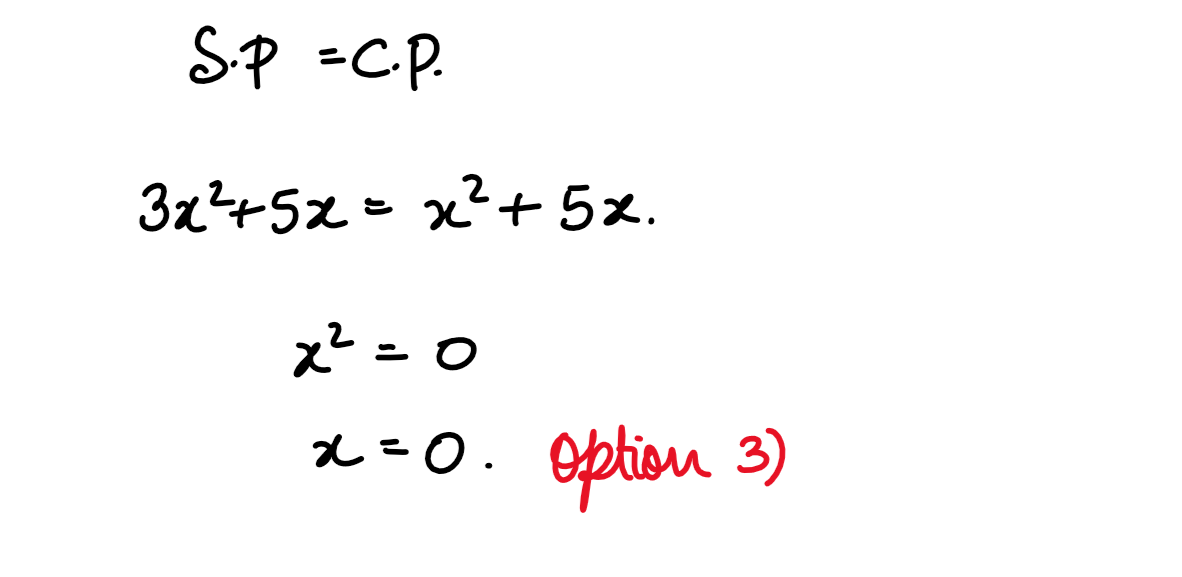




 Free Mock Test Papers
Free Mock Test Papers